The database queue is ideal for scaling long-term activities such as exports, OCR or image processing.
But we should be very careful with database locking if there are more consumers (workers) simultaneously.
How to put item to the queue
It is just simple SQL insert into the database. Just a new record with the right state and request details. It is useful to include some additional information – user id, unique request id, date and time.
INSERT INTO my_queue ...
How to pull item from the queue
This is more tricky because we have to solve concurrency issues. Only one consumer is allowed to grab the specific item at the same time. The correct SQL is:
SELECT * FROM my_queue WHERE state='waiting' FOR UPDATE SKIP LOCKED LIMIT 1
FOR UPDATE – this is important because it locks row during the database transaction. No other consumer will be allowed to process it.
SKIP LOCKED – without this setting, consumer will be waiting until the lock is released, so we would lose parallel processing.
LIMIT 1 – we want to lock and process just only one row, not complete table.
Note: The SQL syntax comes from PostgreSQL database. Other databases may have a different syntax.
Database transaction
We have to use database transaction when pulling the item from the queue. We have two options:
- One long transaction.
- Two short transactions.
One long transaction
BEGIN //find some work SELECT * FROM my_queue WHERE state='waiting' FOR UPDATE SKIP LOCKED LIMIT 1 //do requested work - we are still in the database transaction //no other worker has access to the selected item because of lock //put info we are done UPDATE my_queue SET state='done' WHERE queue_item_id=:id COMMIT
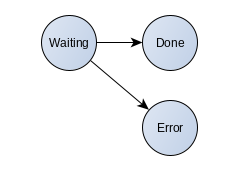
Note: If the worker cannot finish its work, the worker sets error state. We can manually switch to the waiting state if necessary.
Two short transactions
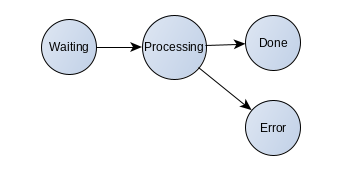
BEGIN //find some work SELECT * FROM my_queue WHERE state='waiting' FOR UPDATE SKIP LOCKED LIMIT 1 //inform others - this item is ours UPDATE my_queue SET state='processing' WHERE queue_item_id=:id COMMIT //do requested work - we are outside of the database transaction //no other worker has access to the selected item because of state BEGIN //inform others - we are done UPDATE my_queue SET state='done' WHERE queue_item_id=:id COMMIT
This solution is better because we do not have a long running database transaction. However if the worker (consumer) fails during the processing – “Out of memory” for example, there will be stuck items in the processing state forever. We will need a special cleaning thread to solve this.
Queue database fields
The recommended database fields in the queue table:
- State – The state of the process.
Waiting,Done,Error,Processing. - Parameters – Parameters for the worker. Can be in JSON format.
- RequestId – Unique ID of the request. It can be defined on API level.
- UserId – ID of user who created the request.
- CreatedDT – Date and time when request was created.
- FinishedDT – Date and time when worker finished its job.
- ErrorMessage – Error message if worker failed.
- WorkerName – The name of the worker. Can be based on hostname for example.
- Result – The result of the worker. It can be UUID of the exported file for example.
- UserContext – What is User Context?
But there is one problem. How consumers find that there is some work to be done? The simple answer is: database notifications.

5 thoughts on “Database queue”